Kontinuität von Kurven und Flächen
Die Kontinuität einer Kurve oder einer Fläche bezieht sich auf die Glätte und Qualität der Form. Die Kontinuität wird durch den Grad der Übereinstimmung zwischen Position, Richtung, Krümmung und Änderungsrate der Krümmung der benachbarten Segmente bestimmt.
Kontinuität von Kurven
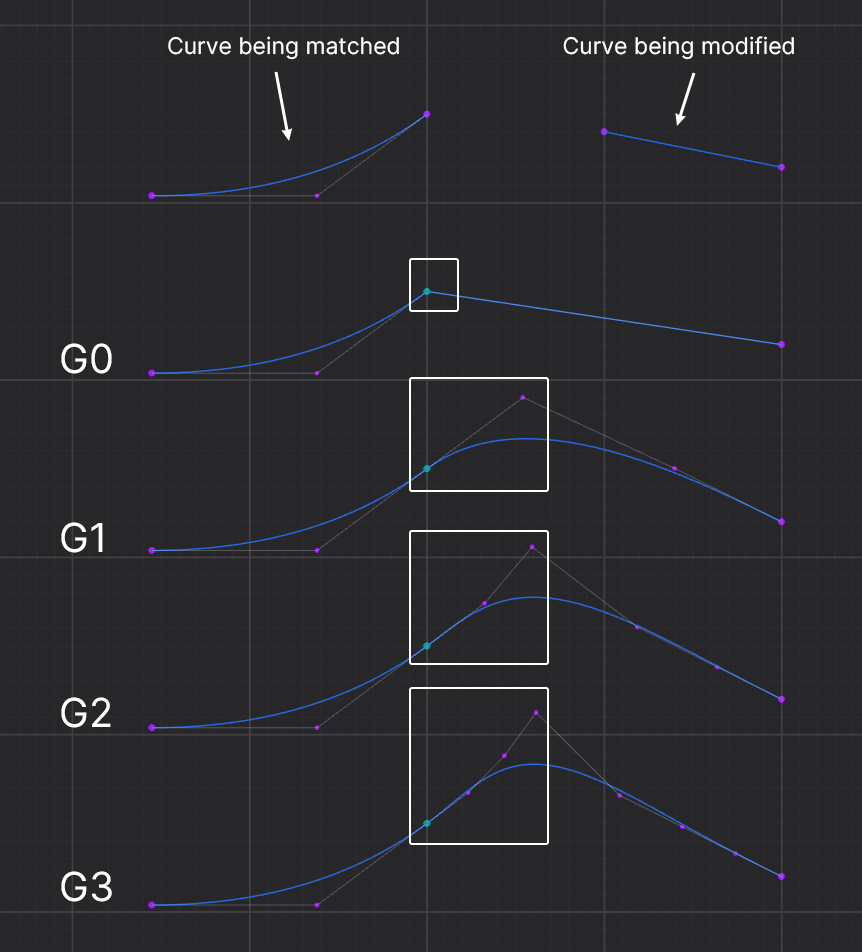
Es gibt vier Stufen der Kurvenkontinuität: G0, G1, G2 und G3.
- G0: Zwei Kurven sind verbunden, aber nur ihre Positionen stimmen am Verbindungspunkt überein.
- G1: Zwei Kurven sind verbunden und ihre Positionen und Richtungen stimmen am Verbindungspunkt überein.
- G2: Zwei Kurven sind verbunden und ihre Positionen, Richtungen und Krümmungen stimmen am Verbindungspunkt überein.
- G3: Zwei Kurven sind verbunden und ihre Positionen, Richtungen, Krümmungen und Krümmungsänderungsraten stimmen am Verbindungspunkt überein.
Höhere Kontinuität ist erforderlich, um glattere und natürlichere Kurven zu erzeugen.
Kontinuität von Flächen
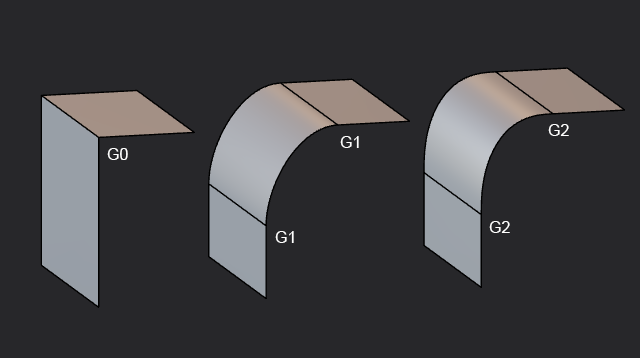
Es gibt drei Stufen der Flächenkontinuität: G0, G1 und G2.
- G0: Zwei Flächen sind verbunden, aber nur ihre Positionen stimmen am Verbindungspunkt überein.
- G1: Zwei Flächen sind verbunden und ihre Positionen und Tangenten stimmen am Verbindungspunkt überein.
- G2: Zwei Flächen sind verbunden und ihre Positionen, Tangenten und Krümmungen stimmen am Verbindungspunkt überein.
Höhere Kontinuität ist erforderlich, um glattere und natürlichere Flächen zu erzeugen.
Referenzvideos
Diese Videos nutzen Anwendungen, die nicht Plasticity sind, zu Demonstrationszwecken, aber die Konzepte können auch auf die Bedienung von Plasticity angewendet werden, daher werden sie hier als Referenz bereitgestellt.
"Kurve und Flächenkontinuität" - CMU PDET
Zusammenfassung
Der Film diskutiert die Feinheiten von Kurven- und Flächenkontinuität und konzentriert sich auf die Typen G0, G1, G2 und G3. Er geht auch auf mathematische Perspektiven, CAD-Systemfähigkeiten und praktische Anwendungen im Design ein, insbesondere in der Automobilindustrie.
Arten von Kontinuität
- G0 Kontinuität: Punkt-Kontinuität, bei der Kurven oder Flächen einen Punkt oder eine Kante teilen, aber unterschiedliche Neigungen haben können.
- G1 Kontinuität: Tangentenkontinuität, bei der es eine G0-Kontinuität gibt und die Neigungen der Kurven gleich sind.
- G2 Kontinuität: Krümmungskontinuität, die G0 und G1 umfasst, plus die Kurven haben die gleiche Krümmungsrate.
- G3 Kontinuität: Fügt eine Beschleunigungskomponente zur G2-Kontinuität hinzu.
Mathematische Perspektive
- G0: Die Funktionen, die die Kurven darstellen, sind an einem bestimmten Punkt nicht gleich.
- G1: Die ersten Ableitungen der Funktionen sind gleich, das bedeutet, sie haben die gleiche Neigung.
- G2: Die zweiten Ableitungen sind gleich und weisen auf die gleiche Krümmungsrate hin.
Visuelle Analysemethoden
- Zebra-Streifen-Analyse: Wird verwendet, um zu bewerten, wie gut Kurven oder Flächen Licht reflektieren.
- Stachelschwein-Analyse: Eine weitere Methode, um die Qualität von Kurven und Flächen visuell zu bewerten.
Standards im Automobildesign
- Class A Flächen: Für den Benutzer sichtbar und erfordern in der Regel G2- oder bessere Kontinuität.
- Class B Flächen: Sichtbar, wenn das Produkt nicht in Gebrauch ist, und haben geringere Kontinuitätsanforderungen.
- Body and White Flächen: Nicht für den Benutzer sichtbar und können G0 oder bessere Kontinuität haben.
Abschließende Bemerkungen
Die Qualität Ihres Designs kann erheblich von der Art der Kontinuität beeinflusst werden, die Sie wählen. Dies gilt insbesondere in Branchen wie dem Automobildesign, wo ästhetische und funktionelle Aspekte von entscheidender Bedeutung sind.